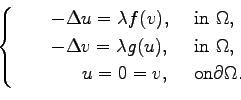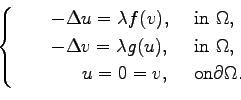Multiple Positive Solutions for Classes of Elliptic Systems
Jaffar Ali Shahul Hammed
Mississippi State University
js415@ra.msstate.edu
Abstract: We study the existence of multiple positive
solutions to systems of the form
Here 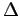 is the Laplacian operator,
is the Laplacian operator, 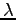 is a positive parameter,
is a positive parameter,
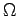 is a bounded domain in
is a bounded domain in
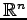 with smooth boundary and
with smooth boundary and 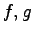 belongs to a class of positive functions that have a combined sublinear effect
at
belongs to a class of positive functions that have a combined sublinear effect
at 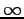 . Our results also easily extend to the corresponding p-Laplacian
systems. We prove our results by the method of sub and super solutions.
. Our results also easily extend to the corresponding p-Laplacian
systems. We prove our results by the method of sub and super solutions.
Summer School 2006
2006-05-09