Prabhu Janakiraman
University of Illinois, Urbana-Champaign
pjanakir@math.uiuc.edu
Abstract: Let  denote the Beurling-Ahlfors transform
defined on
denote the Beurling-Ahlfors transform
defined on  ,
,
 by
by
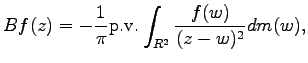 |
(1) |
The celebrated conjecture of T. Iwaniec states that its  norm
norm
 where
where
 . In this paper, the new
upper estimate
is found using martingale methods and further analysis. This is joint work
with Rodrigo Ba
. In this paper, the new
upper estimate
is found using martingale methods and further analysis. This is joint work
with Rodrigo Ba uelos.
uelos.
![]() denote the Beurling-Ahlfors transform
defined on
denote the Beurling-Ahlfors transform
defined on ![]() ,
,
![]() by
by