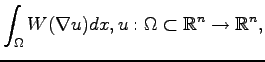
In the study of solid-solid phase transitions and in particular of shape-memory alloys one is interested in studying variational models of the form
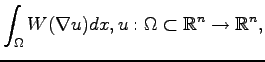
where the energy density ![]() is invariant under rotations and it is minimized
by several copies of the set
is invariant under rotations and it is minimized
by several copies of the set ![]() of the proper rotations, i.e., by sets of
the form
of the proper rotations, i.e., by sets of
the form
While the set ![]() (case
(case ![]() ) is rigid, in the sense that there are no
nontrivial gradient fields taking values in
) is rigid, in the sense that there are no
nontrivial gradient fields taking values in ![]() , the set
, the set ![]() is in general
not rigid.
is in general
not rigid.
After a brief review of known rigidity results, we present a quantitative
rigidity estimate for a multiwell problem (![]() ) in dimension
) in dimension ![]() . Precisely, we show that if a gradient field is
. Precisely, we show that if a gradient field is ![]() -close to the set
-close to the set ![]() ,
a set of the form
,
a set of the form
![]() , and and an appropriate
bound on the length of the interfaces holds, then the gradient field is
actually close to only one of the wells
, and and an appropriate
bound on the length of the interfaces holds, then the gradient field is
actually close to only one of the wells ![]() . The estimate holds for any
connected subdomain, and has the optimal scaling.
. The estimate holds for any
connected subdomain, and has the optimal scaling.
Results of these kind have several applications, e.g., in studying the scaling
of singularly perturbed problem under Dirichlet boundary conditions or in
proving compactness and ![]() -convergence for a sequence of singularly
perturbed functionals of the kind
-convergence for a sequence of singularly
perturbed functionals of the kind
![$\displaystyle I_\varepsilon[u]:=\int \frac{1}{\varepsilon} W(\nabla u) + \varepsilon \vert\nabla^2 u\vert^2 dx.$](img13.png)